Pythagorova věta
1. Strana čtverce měří 6 cm. Vypočítej, o kolik % je úhlopříčka tohoto čtverce větší než jeho strana.
41,6 % ]
2. Čtverec má úhlopříčku dlouhou 18,2 cm. Vypočítej obvod a obsah čtverce.
o = 52 cm; S = 169 cm2
3. Kvádr s obdélníkovou podstavou o rozměrech 21 cm a 28 cm má výšku 84 cm. Vypočítej:
a) velikost úhlopříčky podstavy u = 35 cm
b) velikost tělesové úhlopříčky ut = 91 cm
c) povrch kvádru ( uveď jej v m2 ) S = 0,94 m2
d)
objem kvádru ( uveď jej v litrech ) V = 49,39 l
4. Kolik tun sena se vejde na půdu stodoly 12 m dlouhé a 8 m široké, když výška trojúhelníkového štítu je 3,5 m ? 1 m3 lisovaného sena má hmotnost 105 kg. Z bezpečnostních důvodů může být prostor zaplněn jen do tří čtvrtin.
13,23 t
5. Vypočítej obsah pravoúhlého rovnoramenného trojúhelníku s přeponou c délky 10 cm.
25 cm2
6. V trojúhelníku ABC platí: tb = 7,5 cm, vc = 13,8 cm, ta = 18 cm a těžnice ta a tb jsou vzájemně kolmé. Vypočti obsah trojúhelníku.
89,7 cm2
7. Strana čtverce má délku 6 cm. Vypočti, o kolik % je úhlopříčka tohoto čtverce delší než jeho strana.
asi o 41 %
8. Vypočítej tělesovou úhlopříčku krychle o hraně 8 cm. Počítej s přesností na milimetry.
[ut = 3,9 cm ]
9. Vypočítej povrch krychle, je-li její tělesová úhlopříčka u = 8 cm.
S = 128 cm2
10. Délka jedné odvěsny pravoúhlého trojúhelníka se rovná 75 % délky druhé odvěsny. Urči obvod tohoto trojúhelníku, je-li jeho obsah 24 cm2.
24 cm
11. Urči
obsah lichoběžníku ABCD, je-li dáno: | BC | = ![]() cm, | CD | = 4 cm, | AD | =
cm, | CD | = 4 cm, | AD | = ![]() cm, výška v = 3 cm,
pro základny lichoběžníku platí | AB | > | CD |.
cm, výška v = 3 cm,
pro základny lichoběžníku platí | AB | > | CD |.
S = 16,5 cm2
12. Je dán kvádr ABCDEFGH o rozměrech: | AB | = a = 8 cm, | BC | = b = 8 cm, | BF | = c = 12 cm.
a) Urči délku lomené čáry HZB, kde Z je střed hrany AE. 20 cm
b) Urči obsah trojúhelníku BXF, kde X je střed FG. 24 cm2
c) Kolik procent objemu uvedeného kvádru tvoří objem kvádru s polovičními hranami ?
12,5 %
13. Rovnoramenný lichoběžník má základny 13 cm a 5 cm a výšku 3 cm. Vypočítej délku ramene, délku úhlopříčky a obsah lichoběžníku.
b = 5 cm; u = 9,49 cm; S = 27 cm2
14. Strom vysoký 8 m byl větrem zlomen tak, že se jeho vrchol dotýká země 4 m od kmene. V jaké výšce byl strom zlomen ? Ve výšce 3 m
Pythagorova věta, mocniny
A
1. Vypočítej:
a) 2a2 + 3a2 =
b) ( a3 )2 =
c) ( b4 )3 =
d)
![]()
e) ( -4b2 )3 =
f) ( -3x4 )4 =
g) ( 3a3 )2 =
h)
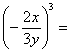
i) ( 3x4 )3 =
j) ( -5a2 )3 =
k) 21a8 : 7a2 =
l)
![]()
m)
![]()
n)
![]()
o) ( 2a . 5b )3 =
2. Vypočítej:
a) 15a2 – 9a – 14a + 23a2 =
b) 0,5 . ( 4x2 – 3x – 9x + 12 ) =
c) ( 3a – 2b )2 : ( 3a – 2b )5 =
d) ( 2a – 4b )8 : ( 2a – 4b )2 =
3. Vypočítej:
a) 5a3 . 3a4 =
b) 8a3 . 9b6 =
c) 3a4. 3a4.3a4 =
d) ( 5a3b5. 4a4b2 )3 =
e) 8a4. 3a2.5a3 =
f) 28m8 : 7m4 =
g) ( 4a )3 . ( 4a )2 =
4. Vypočítej výšku rovnoramenného trojúhelníku ( c = základna, a = rameno )
a = 54 mm, c = 46 mm
5. Je dán pravoúhlý trojúhelník ABC s pravým úhlem při vrcholu C. Vypočítej velikost zbývající strany, je-li dáno: c = 122 mm, a = 22 mm, b = ?
6. Kosočtverec má stranu a = 45 cm a úhlopříčku e = 80 cm. Vypočítej velikost druhé úhlopříčky f.
7. Jak dlouhé je zábradlí u schodiště se 17 schody, je-li schod 32 cm široký a 14,5 cm vysoký ? (Poslední schod se nepočítá.)
Pythagorova věta, mocniny
B
1. Vypočítej:
a) 3a2 . 3a2 =
b) 5a2 + 5a2 =
c) ( a3 )4 =
d) ( 12a3 )2 =
e)
![]()
f)
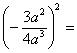
g)
![]()
h)
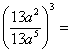
i)
![]()
j)
![]()
k)
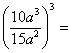
l)
![]()
m)
![]()
n)
![]()
o)
![]()
2. Vypočítej:
a) 5a2 . 3b3 =
b) 3a2 . 3a2 . 3a2 =
c) ( 3a )4 : ( 3a )3 =
d) 16x3 y2 z : 8xy3z4 =
3. Vypočítej:
a)
![]()
b)
![]()
c)
![]()
d)
![]()
e)
![]()
f)
![]()
g) 0,4 . ( 3a2 –2a + 9a – 6 ) =
4. Vypočítej výšku rovnostranného trojúhelníku o straně a = 18 cm.
5. Je dán pravoúhlý trojúhelník ABC s pravým úhlem při vrcholu C. Vypočítej velikost zbývající strany, je-li dáno: c = 50 cm, b = 14 cm, a = ?
6. V pravoúhlém trojúhelníku ABC je dána odvěsna a = 36 cm a obsah S = 540 cm2. Vypočítej velikost přepony.
7. Ve vzdálenosti 12 km od přímé trati je dělo, které dostřelí do vzdálenosti 20 km. Jak dlouhá část trati je v dostřelu ?